Understanding When a Limit Does Not Exist
Limits are fundamental in calculus, providing insights into the behavior of functions as they approach specific points. However, there are situations where a limit does not exist (DNE). This article explores the various scenarios in which limits fail to exist, along with examples and explanations.
1. Definitions and Concepts
A limit describes the value that a function approaches as the input approaches a certain point. Mathematically, we express this as:
where L is the value that f(x) approaches as x approaches a. A limit does not exist when the function does not approach a single finite value.
2. Scenarios Where Limits Do Not Exist
2.1 Jump Discontinuity
A jump discontinuity occurs when the left-hand limit and right-hand limit at a point do not equal each other. For example, consider the piecewise function:
Here,
Since these two limits are not equal, we conclude that:
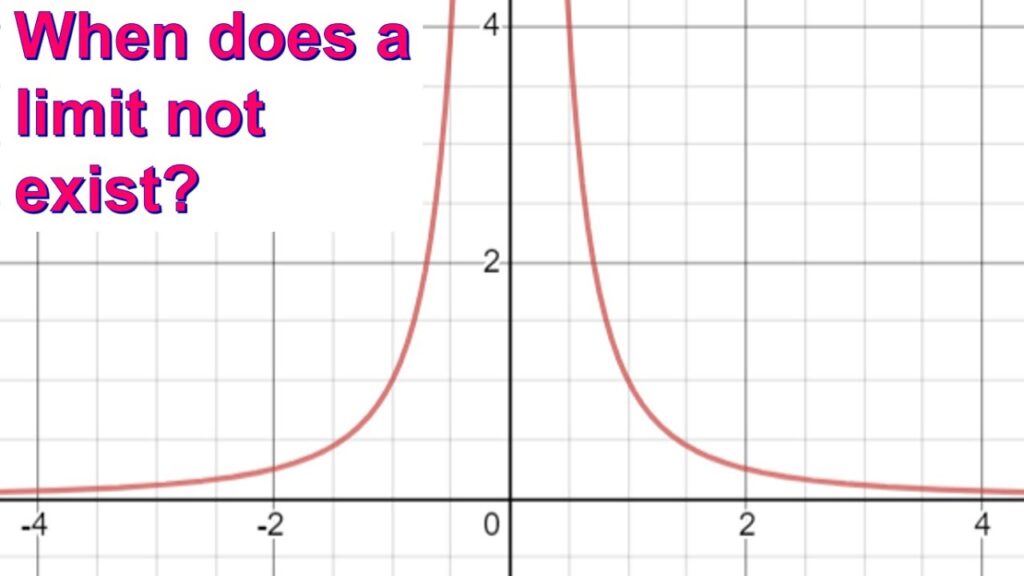
2.2 Infinite Limits
An infinite limit occurs when the function approaches infinity or negative infinity as it approaches a certain point. For instance, consider:
As x approaches 0 from the right, f(x) approaches positive infinity:
Conversely, as x approaches 0 from the left, it approaches negative infinity:
In this case, since one side approaches positive infinity and the other negative infinity, we say that:
2.3 Oscillating Functions
Limits can also fail to exist due to oscillation. A classic example is the function:
As x approaches 0, this function oscillates between -1 and 1 infinitely often. Therefore,
2.4 Vertical Asymptotes
When a function has a vertical asymptote at a point, it means that it approaches infinity or negative infinity at that point. For example:
The function has vertical asymptotes at odd multiples of π2. Thus,
3. Examples and Graphical Representation
To better understand when limits do not exist, let’s look at some graphical representations of functions.
| Function | Type of DNE | Description |
|---|---|---|
| f(x)=1x | Infinite Limit | Approaches infinity as x→0+, and negative infinity as x→0−. |
| Piecewise Function | Jump Discontinuity | Left-hand limit differs from right-hand limit at specific points. |
| f(x)=sin(1x) | Oscillation | Oscillates infinitely as x→0. |
| f(x)=tan(x) | Vertical Asymptote | Approaches infinity at odd multiples of π2. |
4. Frequently Asked Questions (FAQ)
4.1 What does it mean when we say a limit does not exist?
A limit does not exist when a function fails to approach a single finite value as the input approaches a specific point.
4.2 Can limits exist at points of discontinuity?
Yes, limits can exist at points of discontinuity if the left-hand and right-hand limits are equal.
4.3 How do I determine if a limit exists?
You can determine if a limit exists by evaluating one-sided limits and checking for continuity or using graphical analysis.
4.4 Are there any rules for dealing with limits that do not exist?
Common strategies include analyzing one-sided limits or using L’Hôpital’s Rule for indeterminate forms.
4.5 Where can I learn more about limits?
For further reading on limits and their properties, you can visit Wikipedia on Limits.
Conclusion
Understanding when limits do not exist is crucial in calculus and mathematical analysis. By recognizing scenarios such as jump discontinuities, infinite limits, oscillations, and vertical asymptotes, one can better navigate complex functions and their behaviors near critical points.This comprehensive overview highlights key concepts and provides clarity on an essential topic in mathematics.