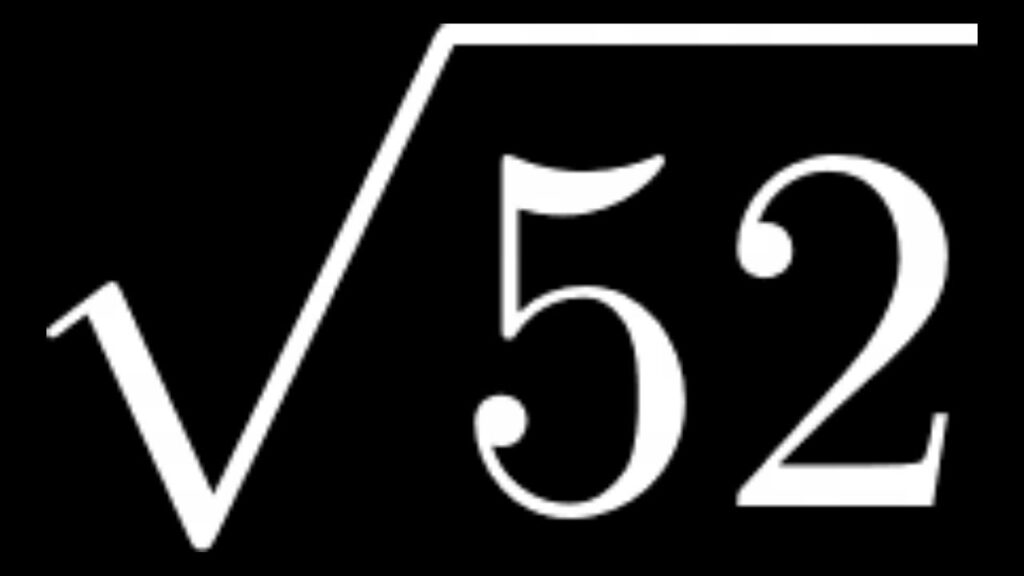Understanding the Square Root of 52
The square root of a number is a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. In this article, we will explore the square root of 52, including its mathematical properties, methods for calculating it, and its significance in various contexts. We will also address frequently asked questions and provide a summary table for quick reference.
What is the Square Root of 52?
The square root of 52 is denoted as 52. It can be expressed in different forms:
- Decimal Form: The square root of 52 is approximately 7.211102551.
- Radical Form: It can be simplified to 213 by factoring out the perfect square from 52.
- Exponential Form: It can also be represented as 520.5 or (52)1/2.
Calculating the Square Root of 52
To find the square root of 52, we can use several methods, including prime factorization, the approximation method, and the long division method.
1. Prime Factorization Method
To use the prime factorization method, we first need to factor 52 into its prime components:
- 52=2×26
- 26=2×13
Thus, the prime factorization of 52 is:
Now, we can take the square root:
This means that the square root of 52 can be expressed in radical form as 213.
2. Approximation Method
To estimate the square root of 52, we can find two perfect squares between which 52 lies. The perfect squares are:
- 72=49
- 82=64
Since 49<52<64, we know:
To get a more precise estimate, we can use the following formula:
Substituting the values:
Therefore, we can estimate:
3. Long Division Method
The long division method can also be used to find the square root of 52. Here’s a step-by-step breakdown:
- Group the digits: Since 52 has two digits, we consider it as one group.
- Find the largest square: The largest square less than or equal to 52 is 72=49.
- Subtract: 52−49=3.
- Bring down a pair of zeros: Treat the remainder as 300 (adding two zeros).
- Double the quotient: Double the 7 to get 14.
- Find the next digit: Determine a digit n such that (14n)n≤300. Here, n=2 works since 142×2=284.
- Subtract again: 300−284=16.
- Bring down another pair of zeros: Now consider 1600.
- Repeat the process: Continue this process to get more decimal places.
Using this method, you can find that 52 approximates to 7.211.
Properties of the Square Root of 52
- Irrational Number: The square root of 52 is an irrational number because it cannot be expressed as a fraction of two integers. Its decimal representation is non-terminating and non-repeating.
- Real Number: As a square root of a positive number, 52 is a real number.
- Approximation: The square root of 52 can be approximated to several decimal places, with a common approximation being 7.2111.
Applications of the Square Root of 52
Understanding the square root of 52 can be useful in various mathematical contexts, including:
- Geometry: Calculating distances or lengths in geometric problems.
- Statistics: Finding standard deviations or variances in data sets.
- Algebra: Solving equations that involve square roots.
Frequently Asked Questions (FAQs)
Q: What is the exact value of the square root of 52?
A: The exact value in radical form is 213, and the approximate decimal value is 7.2111.
Q: Is the square root of 52 a rational number?
A: No, the square root of 52 is an irrational number because it cannot be expressed as a fraction of two integers.
Q: How can I simplify the square root of 52?
A: You can simplify 52 to 213 by factoring out the perfect square.
Q: Can you calculate the square of the square root of 52?
A: Yes, the square of the square root of 52 is simply 52, as (52)2=52.
Q: How do I find the square root of 52 using a calculator?
A: Enter “52” into the calculator and press the square root function (often labeled as or a similar symbol).
Q: What are some other square roots close to 52?
A: The square roots of 49 and 64 are 7 and 8, respectively, which are the nearest perfect squares to 52.
Conclusion
The square root of 52 is an important mathematical concept that can be calculated using various methods, including prime factorization, approximation, and long division. Understanding its properties and applications can enhance your mathematical skills and problem-solving abilities. Whether you are a student, teacher, or simply someone interested in mathematics, knowing how to work with square roots is a valuable skill.For more information on square roots and related mathematical concepts, you can visit the Wikipedia page on Square Roots.
Summary Table
| Property | Value |
|---|---|
| Square Root of 52 | 52≈7.2111 |
| Radical Form | 213 |
| Exponential Form | 520.5 |
| Type | Irrational Number |
| Nearest Perfect Squares | 49 (7) and 64 (8) |
| Applications | Geometry, Statistics, Algebra |