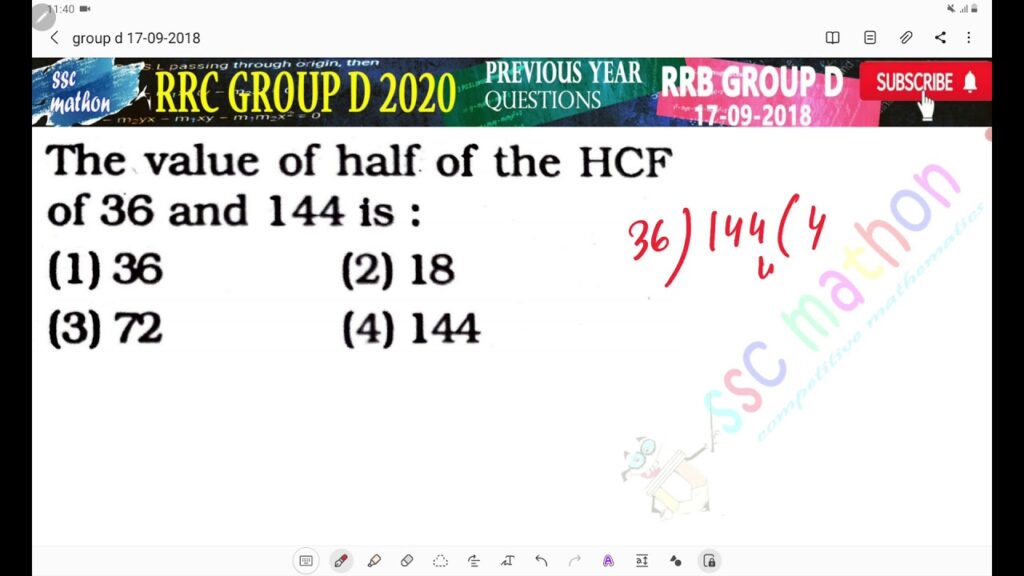
Understanding the Concept of Half of 36
When we talk about “half of 36,” we are essentially discussing a basic mathematical operation known as division. The term “half” refers to dividing a quantity into two equal parts. In this case, we want to find out what one of those equal parts is when the whole is 36.
Basic Calculation
To find half of 36, we can use the following mathematical expression:
Calculating this gives us:
Thus, half of 36 is 18.
Importance of Understanding Halves
Understanding how to calculate halves is fundamental in various aspects of mathematics and daily life. Here are some reasons why knowing how to find half of a number is important:
- Basic Arithmetic Skills: It enhances basic arithmetic skills, which are essential for more complex mathematical operations.
- Real-Life Applications: Knowing how to find halves can be useful in cooking (e.g., halving a recipe), budgeting (e.g., splitting costs), and measuring (e.g., dividing quantities).
- Foundation for Fractions: Understanding halves lays the groundwork for learning about fractions, ratios, and proportions.
Applications of Halves in Everyday Life
Cooking and Baking
In cooking, recipes often require halving ingredients. For example, if a recipe calls for 36 ounces of flour, knowing that half would be 18 ounces allows for adjustments based on serving sizes.
Budgeting and Finance
When managing finances, individuals may need to split expenses. For instance, if a bill is $36, each person would pay $18 if shared equally.
Measurement and Construction
In construction or crafting, measurements often need to be halved. If a piece of wood is 36 inches long, cutting it in half results in two pieces that are each 18 inches long.
Education
In educational settings, understanding how to find halves is essential for teaching students about fractions, ratios, and basic arithmetic. It helps build a strong mathematical foundation.
Visual Representation of Halves
To better understand the concept of halves, visual aids can be helpful. Below are some examples of how to represent halves visually:
Factors Influencing the Concept of Halves
While the mathematical operation of finding half is straightforward, various factors can influence how we apply this concept in real life:
Context
The context in which we find halves can change the way we approach the calculation. For example, halving a recipe requires understanding the ingredients, while splitting a bill involves understanding the total amount and the number of people sharing it.
Precision
In some situations, precision is crucial. For example, in scientific experiments, halving a measurement must be done accurately to ensure valid results.
Rounding
When dealing with odd numbers or quantities that cannot be evenly divided, rounding may be necessary. For instance, if you need to halve 35, you would get 17.5, which may need to be rounded up or down depending on the context.
Common Misconceptions About Halves
Misconception 1: Half Means Just Dividing by Two
While halving a number typically involves dividing by two, it’s essential to consider the context. For example, halving a recipe may require additional adjustments based on the ingredients used.
Misconception 2: Halves Always Result in Whole Numbers
Halves do not always result in whole numbers. For instance, half of 37 is 18.5. Understanding this helps in various applications, such as cooking and measuring.
Misconception 3: Halves Are Only Applicable to Whole Numbers
The concept of halves applies to fractions and decimals as well. For example, half of 0.5 is 0.25, and half of 1/4 is 1/8.
Conclusion
In conclusion, half of 36 is 18. Understanding how to calculate halves is a fundamental mathematical skill with numerous applications in daily life, including cooking, budgeting, and measurement. By grasping the concept of halves, individuals can enhance their arithmetic skills and apply this knowledge in practical situations.
FAQ Section
Q1: What is half of 36?
A1: Half of 36 is 18.
Q2: How do you calculate half of a number?
A2: To calculate half of a number, divide the number by 2. For example, half of 36 is calculated as 36÷2=18.
Q3: Why is understanding halves important?
A3: Understanding halves is important for basic arithmetic skills, real-life applications (like cooking and budgeting), and laying the foundation for learning about fractions and ratios.
Q4: Can halves be represented visually?
A4: Yes, halves can be represented visually using pie charts, number lines, and other graphical methods to illustrate the concept of dividing a whole into two equal parts.
Q5: Are there situations where halves do not result in whole numbers?
A5: Yes, when halving odd numbers or fractions, the result may not be a whole number. For example, half of 35 is 17.5.
Q6: How can I apply the concept of halves in cooking?
A6: In cooking, you can use the concept of halves to adjust recipes. For example, if a recipe calls for 36 ounces of an ingredient, you can use 18 ounces if you want to make half the recipe.
Q7: What is half of an odd number?
A7: Half of an odd number results in a decimal or fraction. For example, half of 37 is 18.5.
Q8: Can the concept of halves apply to decimals?
A8: Yes, the concept of halves applies to decimals as well. For example, half of 0.6 is 0.3.
Q9: How can I practice finding halves?
A9: You can practice finding halves by taking various numbers and dividing them by 2, including whole numbers, fractions, and decimals.
Q10: Where can I find more information about basic arithmetic concepts?
A10: For more detailed information on basic arithmetic concepts, you can visit the Wikipedia page dedicated to arithmetic.
Summary Table
| Concept | Calculation | Result |
|---|---|---|
| Half of 36 | 36÷2 | 18 |
| Half of 35 | 35÷2 | 17.5 |
| Half of 0.6 | 0.6÷2 | 0.3 |
| Half of 1/4 | 14÷2 | 18 |
This article provides a thorough understanding of the concept of halves, specifically focusing on the calculation of half of 36. By grasping this fundamental concept, individuals can enhance their mathematical skills and apply them in various real-life situations.