Unraveling the Mysteries of the Rhombus: A Comprehensive Exploration
In the vast and intricate world of geometry, the rhombus stands out as a unique and captivating shape. With its distinctive four-sided, equiangular structure, the rhombus has captured the attention of mathematicians, architects, and artists alike. In this comprehensive article, we will delve into the fascinating properties, applications, and historical significance of the rhombus, providing a deeper understanding of this remarkable geometric form.
The Definition and Properties of a Rhombus
A rhombus is a quadrilateral, or a four-sided polygon, in which all four sides are of equal length. Additionally, the opposite sides of a rhombus are parallel, and the opposite angles are also equal. This unique combination of properties sets the rhombus apart from other quadrilaterals, such as the square, rectangle, and parallelogram.The key properties of a rhombus include:
- Equiangular: A rhombus has four equal angles, each measuring 60 or 120 degrees.
- Equilateral: All four sides of a rhombus are of equal length.
- Opposite sides are parallel: The opposite sides of a rhombus are parallel to each other.
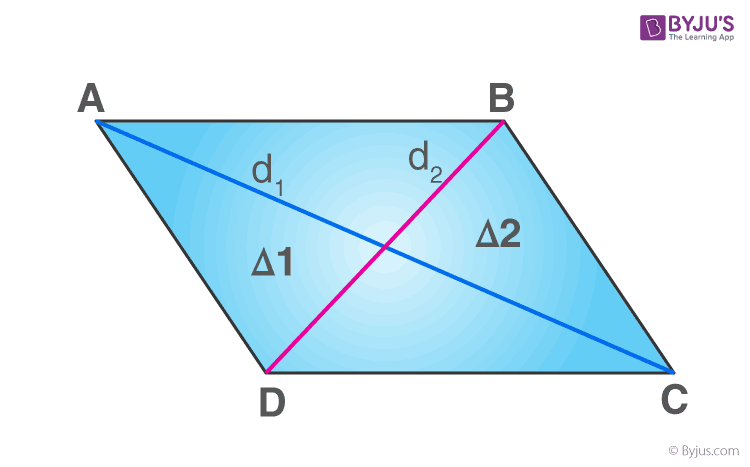
- Diagonals bisect each other at right angles: The two diagonals of a rhombus intersect at right angles and bisect each other.
- Diagonals are perpendicular bisectors: The diagonals of a rhombus are perpendicular bisectors of each other.
These properties, combined with the rhombus’s unique shape, make it a versatile and intriguing geometric form with a wide range of applications.
The History and Origins of the Rhombus
The rhombus has a long and fascinating history, with its origins dating back to ancient civilizations. The earliest known references to the rhombus can be found in the writings of ancient Greek mathematicians, such as Euclid, who discussed the properties of this quadrilateral in his seminal work, “Elements.”In ancient Egypt, the rhombus was used in the construction of various architectural structures, including the Great Pyramid of Giza. The Egyptians recognized the inherent stability and strength of the rhombus, which made it an ideal shape for supporting heavy loads and creating visually striking designs.Throughout history, the rhombus has been employed in a variety of contexts, from religious and cultural symbolism to engineering and design. In the Middle Ages, the rhombus was often used in religious art and architecture, representing concepts such as balance, harmony, and the four elements of the universe.In more recent times, the rhombus has continued to captivate the minds of mathematicians, scientists, and artists, who have explored its properties and applications in fields ranging from geometry and physics to architecture and art.
Applications of the Rhombus
The unique properties of the rhombus have led to its widespread use in a variety of applications, from the practical to the artistic.
Architecture and Engineering
The rhombus’s inherent stability and strength have made it a popular choice in architectural and engineering design. Rhombus-shaped structures, such as domes and vaults, are known for their durability and ability to distribute loads evenly. Additionally, the rhombus has been used in the design of bridges, trusses, and other load-bearing structures.
Art and Design
The rhombus’s visual appeal and symmetry have made it a popular motif in art and design. Rhombus patterns and shapes can be found in textiles, ceramics, jewelry, and various forms of decorative art. Architects and interior designers have also incorporated the rhombus into their work, using it to create visually striking and harmonious spaces.
Mathematics and Science
In the realm of mathematics and science, the rhombus has been the subject of extensive study and analysis. Mathematicians have explored the rhombus’s properties, such as its diagonals, angles, and area, and have applied this knowledge to various fields, including geometry, physics, and computer science.
Everyday Applications
The rhombus can also be found in everyday objects and situations. For example, the diamond shape on playing cards and the shape of certain road signs are both examples of the rhombus in practical use.
Constructing and Measuring a Rhombus
Constructing a rhombus can be a straightforward process, and there are several methods to achieve this. One common approach is to use a compass and straightedge to draw two intersecting lines at equal angles, then connect the endpoints to form the rhombus.Measuring the properties of a rhombus is also an important skill. The key measurements include:
- Side length: The length of each of the four equal sides.
- Diagonal lengths: The lengths of the two diagonals that intersect at right angles.
- Angles: The four equal angles, each measuring 60 or 120 degrees.
- Area: The area of the rhombus, which can be calculated using the formula: Area = (diagonal 1 × diagonal 2) / 2.
Understanding how to construct and measure a rhombus is essential for various applications, from architectural design to mathematical problem-solving.
Frequently Asked Questions (FAQ)
- What is a rhombus?
- A rhombus is a quadrilateral, or a four-sided polygon, in which all four sides are of equal length. The opposite sides of a rhombus are parallel, and the opposite angles are also equal.
- What are the properties of a rhombus?
- The key properties of a rhombus include being equiangular (four equal angles), equilateral (four equal sides), having opposite sides that are parallel, and having diagonals that bisect each other at right angles.
- How is a rhombus different from a square or a rectangle?
- A square is a special case of a rhombus, where all the angles are 90 degrees. A rectangle is a quadrilateral with four right angles, but the sides are not necessarily equal in length.
- What is the history and origin of the rhombus?
- The rhombus has been known since ancient times, with references to its properties found in the writings of ancient Greek mathematicians like Euclid. The rhombus was also used in ancient Egyptian architecture and has been employed in various cultural and religious contexts throughout history.
- What are some applications of the rhombus?
- The rhombus has been used in architecture and engineering for its stability and load-bearing properties, in art and design for its visual appeal, and in mathematics and science for its unique geometric properties.
- How do you construct a rhombus?
- One common method for constructing a rhombus is to use a compass and straightedge to draw two intersecting lines at equal angles, then connect the endpoints to form the rhombus.
- How do you measure the properties of a rhombus?
- The key measurements of a rhombus include the side length, diagonal lengths, angles, and area. The area can be calculated using the formula: Area = (diagonal 1 × diagonal 2) / 2.
- Are there any everyday examples of the rhombus?
- Yes, the rhombus can be found in everyday objects and situations, such as the diamond shape on playing cards and the shape of certain road signs.
- What is the significance of the rhombus in mathematics and science?
- In mathematics and science, the rhombus has been the subject of extensive study and analysis, with its properties being applied to various fields, including geometry, physics, and computer science.
- Can the rhombus be used in art and design?
- Yes, the rhombus’s visual appeal and symmetry have made it a popular motif in art and design, with rhombus patterns and shapes being incorporated into textiles, ceramics, jewelry, and various forms of decorative art, as well as architectural and interior design.
Comparison of Quadrilaterals
| Quadrilateral | Sides | Angles | Diagonals |
|---|---|---|---|
| Square | 4 equal sides | 4 right angles | Perpendicular, equal length |
| Rectangle | Opposite sides equal | 4 right angles | Perpendicular, unequal length |
| Parallelogram | Opposite sides equal | Opposite angles equal | Bisect each other |
| Rhombus | 4 equal sides | Opposite angles equal | Perpendicular, bisect each other |
Source: Wikipedia – Quadrilateral
Conclusion
The rhombus, with its unique and captivating properties, has captured the attention of mathematicians, architects, and artists throughout history. From its ancient origins to its modern-day applications, the rhombus continues to fascinate and inspire those who seek to understand the intricacies of the geometric world.