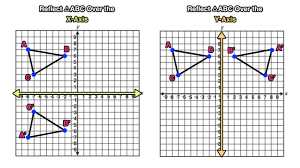
How To Reflect Over X Axis

How to Reflect Over the X-Axis: A Comprehensive Guide

Reflection is a fundamental concept in geometry that involves flipping a figure over a specified line, creating a mirror image of the original shape. This article will provide an in-depth exploration of how to reflect points and shapes over the x-axis, including the mathematical principles involved, step-by-step instructions, examples, and a FAQ section.

Table of Contents

1. Understanding Reflection
2. Mathematical Principles of Reflection
3. How to Reflect Over the X-Axis
4. Examples of Reflection Over the X-Axis
5. Applications of Reflection in Geometry
6. Common Mistakes When Reflecting
7. Conclusion
8. FAQ Section
9. References

1. Understanding Reflection

In geometry, reflection refers to a transformation that produces a mirror image of a figure across a specified line known as the “line of reflection.” The most common lines of reflection are the x-axis and y-axis. When reflecting over the x-axis, the y-coordinates of points are inverted, while the x-coordinates remain unchanged.

2. Mathematical Principles of Reflection

The mathematical rule for reflecting a point $(x,y)$ over the x-axis is straightforward:

• The new coordinates after reflection will be $(x,-y)$.

This means that the x-coordinate stays the same, while the y-coordinate changes its sign. For example, if a point is located at $(3,5)$, its reflection over the x-axis will be at $(3,-5)$.

3. How to Reflect Over the X-Axis

To reflect a point or a figure over the x-axis, follow these steps:

1. Identify the Points: Determine the coordinates of the points that you want to reflect.
2. Apply the Reflection Rule: For each point $(x,y)$, change the y-coordinate to $-y$ while keeping the x-coordinate the same.
3. Plot the New Points: On a coordinate plane, plot the new points obtained from the reflection.
4. Connect the Points: If reflecting a shape, connect the new points in the same order as the original shape to complete the reflection.

4. Examples of Reflection Over the X-Axis

Example 1: Reflecting a Single Point

Original Point: $(2,3)$Reflection Steps:

• Apply the reflection rule: $(2,3)\to (2,-3)$

Result: The reflected point is $(2,-3)$.

Example 2: Reflecting a Triangle

Original Triangle Vertices:

• A: $(1,2)$
• B: $(3,4)$
• C: $(5,1)$

Reflection Steps:

• A: $(1,2)\to (1,-2)$
• B: $(3,4)\to (3,-4)$
• C: $(5,1)\to (5,-1)$

Reflected Triangle Vertices:

• A’: $(1,-2)$
• B’: $(3,-4)$
• C’: $(5,-1)$

Plotting: Plot points A’, B’, and C’ on the coordinate plane and connect them to form the reflected triangle.

5. Applications of Reflection in Geometry

Reflection is utilized in various fields, including:

• Computer Graphics: Reflection is used to create mirror images in graphic design and animation.
• Robotics: Understanding reflections helps in programming robots to navigate and interact with their environment.
• Architecture: Reflection principles are applied in designing symmetrical structures and layouts.

6. Common Mistakes When Reflecting

1. Neglecting the X-Coordinate: Remember that only the y-coordinate changes; the x-coordinate remains the same.
2. Incorrect Sign Change: Ensure that the y-coordinate is correctly negated; for instance, $(3,5)$ should become $(3,-5)$ and not $(3,5)$.
3. Misplotting Points: When plotting the reflected points, ensure accuracy in their placement on the coordinate plane.

7. Conclusion

Reflecting over the x-axis is a fundamental geometric transformation that is essential for understanding more complex concepts in mathematics. By following the outlined steps and principles, anyone can successfully reflect points and shapes over the x-axis, enhancing their geometric skills.

8. FAQ Section

1. What is reflection in geometry?
   Reflection is a transformation that produces a mirror image of a figure across a specified line, such as the x-axis or y-axis.
2. How do you reflect a point over the x-axis?
   To reflect a point $(x,y)$ over the x-axis, change the y-coordinate to $-y$, resulting in the new point $(x,-y)$.
3. What happens to the x-coordinate when reflecting over the x-axis?
   The x-coordinate remains unchanged during reflection over the x-axis.
4. Can you reflect shapes other than points?
   Yes, you can reflect any geometric shape by applying the same reflection rule to each of its vertices.
5. What is the reflection of the point $(-4,2)$ over the x-axis?
   The reflection of the point $(-4,2)$ over the x-axis is $(-4,-2)$.
6. How do you know if the reflection is correct?
   The reflected image should appear as a mirror image of the original across the line of reflection.
7. What is the significance of reflection in real life?
   Reflection principles are used in various fields, including computer graphics, robotics, and architecture, to create symmetrical designs and navigate spaces.
8. Where can I learn more about reflections in geometry?
   You can find additional resources on reflections in geometry at educational websites and math-focused platforms.

9. References

• Reflection (geometry) – Wikipedia