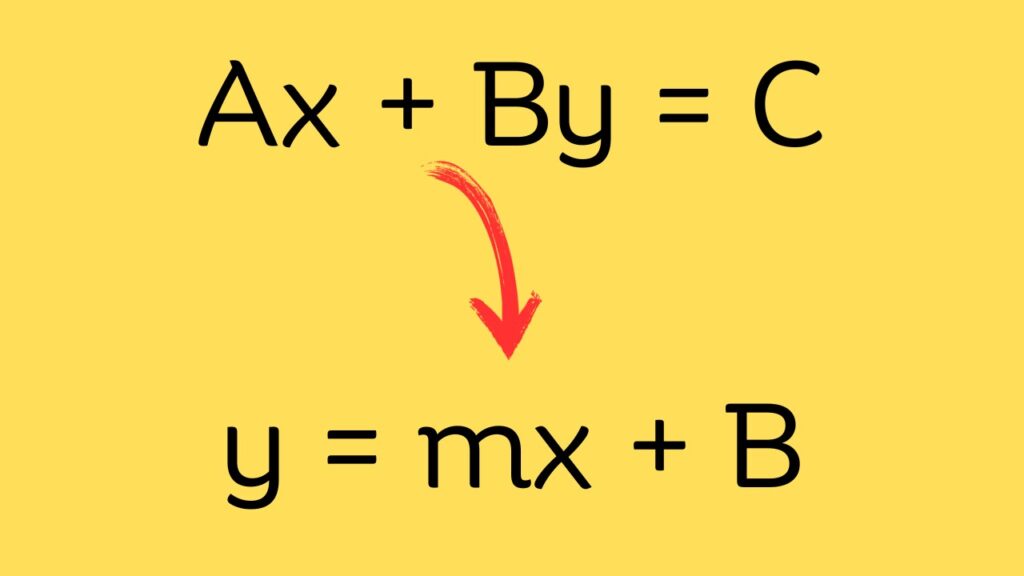Understanding Linear Equations
What is Standard Form?
The standard form of a linear equation is typically expressed as:
where:
- A, B, and C are constants.
- A should be a non-negative integer, and A and B should not both be zero.
What is Slope-Intercept Form?
The slope-intercept form of a linear equation is expressed as:
where:
- m represents the slope of the line.
- b represents the y-intercept, which is the point where the line crosses the y-axis.
Importance of the Conversion
Converting from standard form to slope-intercept form allows for easier graphing and understanding of the linear relationship represented by the equation. The slope-intercept form clearly shows the slope and y-intercept, making it straightforward to plot the line on a graph.
Steps to Convert Standard Form to Slope-Intercept Form
Step 1: Start with the Standard Form Equation
Begin with the standard form of the equation:
Step 2: Isolate the y Variable
To convert to slope-intercept form, you need to solve for y. Start by moving the Ax term to the right side of the equation:
Step 3: Divide by the Coefficient of y
Next, divide every term by B to isolate y:
Step 4: Identify the Slope and Y-Intercept
Now, the equation is in slope-intercept form:
From this equation, you can identify:
- The slope m=−AB
- The y-intercept b=CB
Example Conversions
Example 1: Convert 2x+3y=6
- Start with the equation:
2x+3y=6
- Move 2x to the right:
3y=−2x+6
- Divide by 3:
y=−23x+2
- Slope: −23
- Y-Intercept: 2
Example 2: Convert 4x−y=8
- Start with the equation:
4x−y=8
- Move 4x to the right:
−y=−4x+8
- Multiply by −1:
y=4x−8
- Slope: 4
- Y-Intercept: −8
Example 3: Convert x+2y=4
- Start with the equation:
x+2y=4
- Move x to the right:
2y=−x+4
- Divide by 2:
y=−12x+2
- Slope: −12
- Y-Intercept: 2
Example 4: Convert 3x+5y=15
- Start with the equation:
3x+5y=15
- Move 3x to the right:
5y=−3x+15
- Divide by 5:
y=−35x+3
- Slope: −35
- Y-Intercept: 3
Table: Summary of Conversion Steps
| Step | Action |
|---|---|
| 1. Start with Standard Form | Write the equation in the form Ax+By=C |
| 2. Isolate y | Rearrange to By=−Ax+C |
| 3. Divide by B | Solve for y to get y=−ABx+CB |
| 4. Identify Slope and Intercept | From y=mx+b, find m and b |
Applications of Slope-Intercept Form
Graphing Linear Equations
The slope-intercept form is particularly useful for graphing linear equations. By knowing the slope and y-intercept, you can quickly plot the line:
- Plot the y-intercept on the y-axis.
- Use the slope to determine the rise over run from the y-intercept to find another point on the line.
- Draw the line through the points.
Real-World Applications
Understanding how to convert between forms is essential in various fields, including:
- Economics: Analyzing cost functions and revenue.
- Physics: Understanding motion and forces.
- Engineering: Designing systems and structures.
FAQ Section
Q1: Why do we need to convert standard form to slope-intercept form?
A1: Converting to slope-intercept form makes it easier to graph linear equations and understand their properties, such as slope and y-intercept.
Q2: Can all linear equations be converted to slope-intercept form?
A2: Yes, all non-vertical linear equations can be expressed in slope-intercept form. Vertical lines cannot be represented in this form because their slope is undefined.
Q3: What if B=0 in the standard form?
A3: If B=0, the equation represents a vertical line, which cannot be expressed in slope-intercept form.
Q4: How do I check my conversion is correct?
A4: After converting, you can verify by plugging in values for x and checking if the corresponding y values match the original equation.
Q5: What is the significance of the slope in real life?
A5: The slope represents the rate of change between two variables. For example, in a business context, it can indicate how sales change with respect to advertising spending.
Conclusion
Converting linear equations from standard form to slope-intercept form is a valuable skill in algebra that enhances understanding of linear relationships. By following the outlined steps and practicing with examples, students can master this conversion process. The slope-intercept form not only simplifies graphing but also provides insights into the behavior of linear equations in various applications.For further information on linear equations and their applications, you can visit the Wikipedia page on Linear Equations.